Appearance
分数(Score)
本文的资料来自于官方wiki,但参考osu!stable的源码进行了修改。
计分方式
osu!mania的分数由两部分组成:
主要涉及的数值见下。
下表为判定相关数值:
| 判定 | HitValue[1] | HitBonusValue | HitBonus | HitPunishment |
|---|---|---|---|---|
| max | 320 | 32 | 2 | |
| 300 | 300 | 32 | 1 | |
| 200 | 200 | 16 | 8 | |
| 100 | 100 | 8 | 24 | |
| 50 | 50 | 4 | 44 | |
| miss | 0 | 0 | ∞[2] |
下表为mod相关数值:
| Mod | ModMultiplier |
|---|---|
| Easy | 0.5 |
| NoFail | 0.5 |
| HalfTime | 0.5 |
提示
- std转谱可以使用改变键位数的mod,从1K到9K,它们的ModMultiplier计算方式见下。不过这没有什么影响,反正根本没有人打转谱。如果你在打的话,请立刻停止这种行为。(二次放送)
- 若mod的键数小于谱面原始键数,ModMultiplier为。
- 若等于谱面原始键数,则为1。
- 若大于谱面原始键数,则为0.9。
- 官方wiki给出的上表还有名为ModDivider的值,其意义是开DT、HD、FL等增加难度的mod时,打出不完美判定之后的HitPunishment会减小,但我查阅stable源码之后发现,这些值在游戏中没有定义,在游戏中的实际测试也倾向于这个值其实不存在,因此在本文中我们忽略这个值。
基础分数
一个note的基础分数计算方式如下:
最大分数即mania模式的满分100万。谱面note数为谱面总共note数,普通note和滑条都视为一个。
额外分数
一个note额外分数的计算方式如下:
Bonus值初始时默认为100,且数值限制在之间。
此外,如果某一时刻连击数达到384[3](在滑条中间达到也算),此时Bonus值会直接回复到100。此后的下一个note计算额外分数时,使用到的“上一个note时的Bonus值”就会为100。顺带一提,这是连击数直接影响osu!mania分数的唯一方式。
讨论
⫻Under Construxion⫻
本部分仍在施工中……
为了计算方便,在以下的讨论中,我们统一规定:一个彩300判定得到的基础分数为100分,其他分数则与之保持比例。在此条件下,各种判定的基础分数和额外分数可见下表:
| 判定 | 基础分数 | 额外分数 |
|---|---|---|
| max | 320 | |
| 300 | ||
| 200 | ||
| 100 | ||
| 50 | ||
| miss | 0 | 0 |
顺带一提,如果某张图中一个彩300判定得到的基础分数是100分,那么这张图应该有恰好5000个note。总note数接近这个值的谱面例如4K的Round Wave Crusher - Slash Dot Slash (Slim Boy Fat) (TheToaphster) [-.-][6],或7K著名的飞升天堂[7]。
最大分数
我们试者反过来计算mania的满分。为了看起来更清楚,这里就不使用上面所说的假定谱面有5000个note了,而是设谱面note数为。
可以看出,mania的满分确实为100万分,且其中基础分数和额外分数各占50万分。
不完美判定
不完美判定指200、100、50和miss,这些判定结果没有HitBonus,而有HitPunishment。
| 情形1 | 0 | 1 | 2 | 3 | …… | 50 |
|---|---|---|---|---|---|---|
| 判定 | max | max | max | max | …… | max |
| Bonus值 | 100 | 100 | 100 | 100 | …… | 100 |
| 额外分数 | …… |
| 情形2 | 0 | 1 | 2 | 3 | …… | 50 |
|---|---|---|---|---|---|---|
| 判定 | miss | max | max | max | …… | max |
| Bonus值 | 0 | 2 | 4 | 6 | …… | 100 |
| 额外分数 | 0 | …… |
可见,直到50个note之后,Bonus值才完全恢复到100。在此过程中,基础分数的损失只有100分,而额外分数的损失高达分,这是一个彩300最多能拿到的总共分数的8倍还多[8]。而且这还是(不考虑连击数影响下)一个miss理论上能造成的最小损失——如果其后的判定不全是彩300,而夹杂着黄300或其它不完美判定,额外分数的损失还会增加。
相同情况(该不完美判定之前的Bonus值是100,且在该不完美判定之后的所有判定全为彩300,且不考虑连击数影响)下,各种不完美判定的分数损失见下表(部分值只保留两位小数):
| 判定 | 基础分数 | 额外分数 | 合计 |
|---|---|---|---|
| 200 | 37.5 | 58.11 | 95.61 |
| 100 | 68.75 | 146.98 | 215.73 |
| 50 | 84.38 | 341.64 | 426.02 |
| miss | 100 | 1719.52 | 1819.52 |
可见,对于各种不完美判定,均有额外分数的损失大于基础分数,而且判定越差,额外分数损失会以二次方增长,所占比例越大。与上文一样,这里列出的额外分数损失值也是理论上能造成的最小损失。
对于一种特定的不完美判定,其造成基础分数的损失是恒定的,不会因其他因素而有所区别,因此下文主要讨论额外分数。
不完美判定的位置
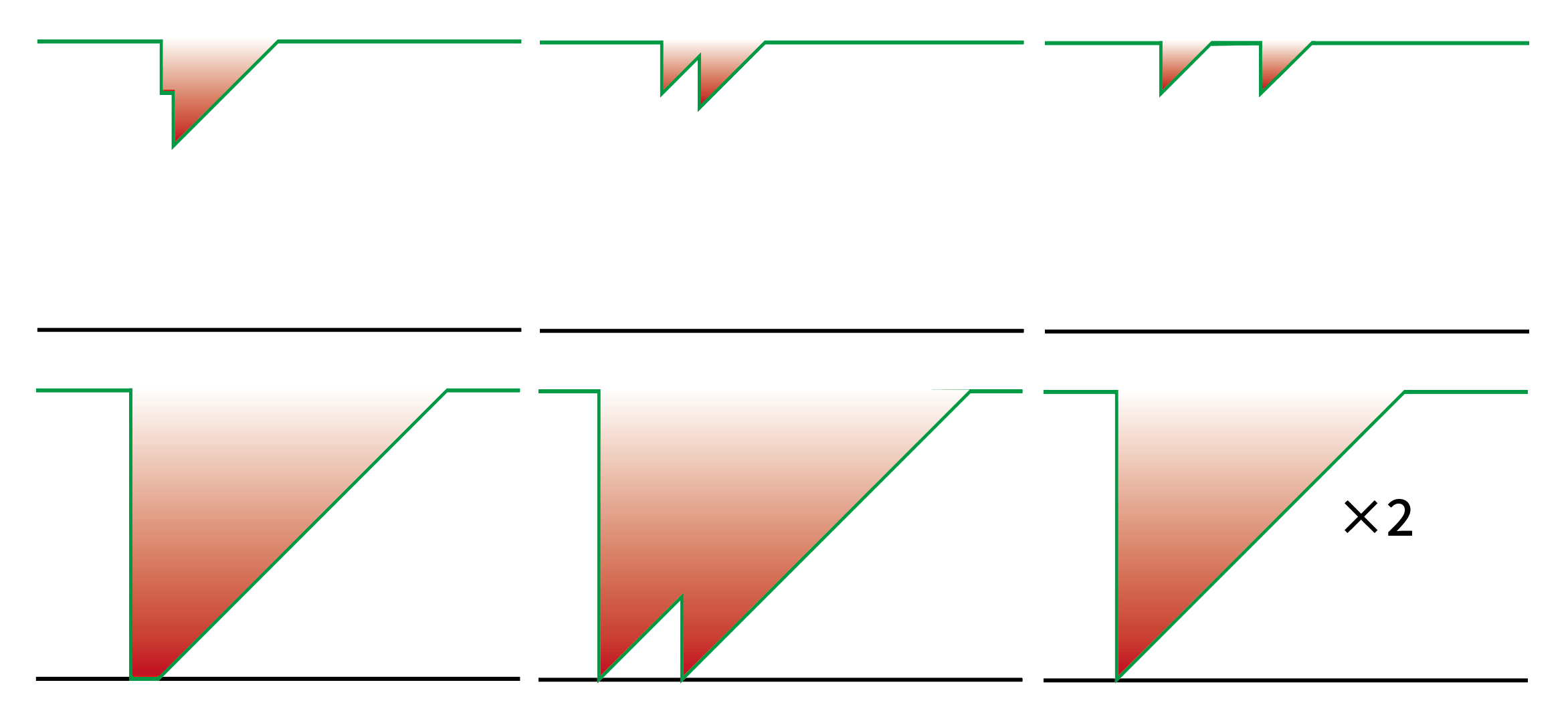
由上文可见,不完美判定对额外分数的主要影响是通过降低bonus值实现的。对于单个不完美判定、Bonus值相同的条件下,只有在不完美判定出现在谱面结尾、剩下的note不足以把Bonus值恢复到100时,不完美判定的损失分数才会减少一些(如下图右侧所示);其他情况下,不完美判定出现的位置不会影响其损失的分数。
这里只讨论对分数的影响——至于说对心态的影响,显然是在谱面快结束时突然miss更大[9]。

不完美判定的分布
200和100多个连续或接近出现时会使bonus值降得更低,恢复需要更长时间,因此对额外分数影响大于相互独立(指在下一个不完美判定出现时,bonus值有足够的时间恢复到100)的200或100,如下图所示,上部从左到右依次为两个连续出现、接近出现和相互独立的200。例如,连续出现的5个200会造成额外分数损失487.28分,这超过了8个相互独立的200造成的额外分数损失[10]。如果有一段图是基本上糊过来的,隔三岔五就蹦出来200或100,只能等着神秘数值——384来挽救一直低空飞行的bonus值,就会对额外分数造成很大的影响。
但对于miss来说,即使单独出现也能够将bonus值降到0,连续出现很多个也不会使bonus降得更低,造成的额外分数损失也基本上和单个miss一样,反而是相互独立的miss会导致更大的损失。
听说你也想做inteliser?
在SS的情况下,bonus值始终为100,彩300与黄300的额外分数都是相同的,此时反而只有基础分数会影响总分。在彩黄比为时,容易得到此时的总分为。彩黄比和分数(单位:万分)的关系见下图。
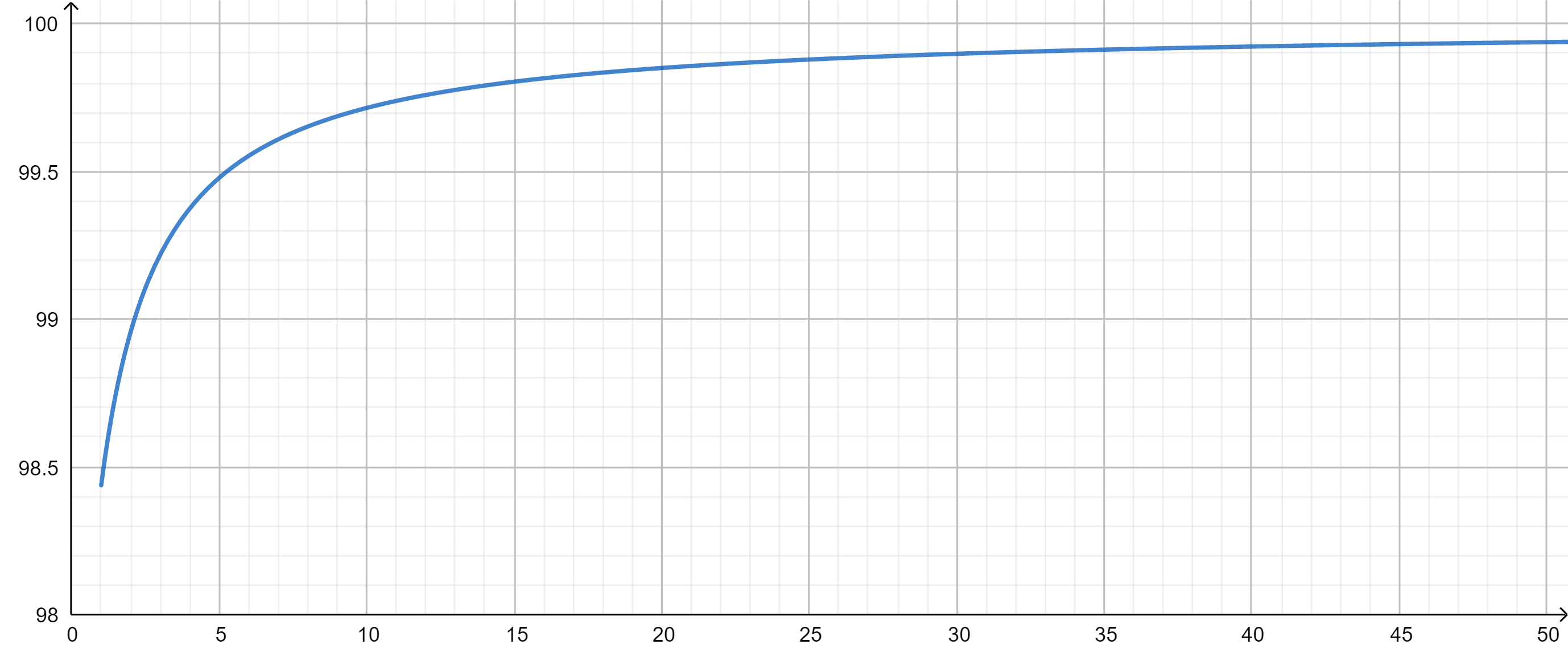
一些常见的目标分数所需的最低彩黄比见下表。
| 目标分数 | 彩黄比 |
|---|---|
| 990,000 | 2.125 |
| 995,000 | 5.25 |
| 999,000 | 30.25 |
| 999,500 | 61.5 |
这些值的名字我实在想不到好的翻译方式,所以只能用原名,十分抱歉。如果有人有好的点子请务必告诉我。 ↩︎
在游戏中,实际上的实现机制是强行将Bonus设定为-56。可是为什么是-56呢?这恐怕是个魔术数字。 ↩︎
为什么是384?又是一个魔术数字。所以我认为立绘不应该在连击数达到100的倍数时出现,而应该达到384的倍数时出现。这样一来,首先出现频率没那么高,而且当你看到Maria酱[4]出现的时候,就象征着:就算之前就算miss再多,准度再烂,这些过去的一切的影响都已经完全消失了——现在你需要做的就只是专注于面对接下来的挑战了。(因为脚注没人看就在其中灌鸡汤的作者是人间之屑) ↩︎
具体是谁可能因为你用的自定义皮肤而有所不同——没错,脚注中也可以加脚注。 ↩︎
总note数5020。 ↩︎
总note数5062。如果你能打这个图,请务必让我膜拜一下。如果你能DT这个图,请让我膜拜1.5下。 ↩︎
要知道以miss惩罚大而著称的etterna,其miss的合计损失也只有完美判定分数的5倍而已。 ↩︎
如果你直到最后一个之前的note全部都连上,结果最后一个断了,你会得到名为“The Sum Of All Fears”的成就。 ↩︎
你可能注意到了,这个损失依然只有一个miss造成的损失的零头。实际上,需要连续出9~10个200或4个100导致的基础+奖励分数损失才能赶得上一个miss。如果要在断连和糊之间选一个的话,很多时候后者更有利。 ↩︎